2022. 9. 12. 17:09ㆍCS/자료구조, 알고리즘
이번 포스팅 내용은 Merge Sort 의 정확성을 증명해보는 것이다.
Divide and Conquer - 분할 정복
- 입력을 나누어 더 작은 문제를 물고, 작은 문제들의 답을 조합해 전체 문제의 답을 만든다.
- 아주 작은 문제는 어쨌거나 풀린다.
mergeSort는 분할 정복 기법을 사용한다. 문제를 더 작은 문제로 나누고, 답을 합칠 때(merge) 재귀가 사용된다.

위처럼 "이미 Sorted 된 두 배열을 합쳐(merge) Sorted 된 배열을 만들자" 가 이 알고리즘의 아이디어이다.
재귀라고 해서 따라 들어가지 않고, 바로 알 수 있도록 증명해보는 연습을 하는 것이다.
Recursive MergeSort
int sort(int a[], int n){
if(n<=1)
return 0;
int h, b[n];
h = n/2;
// copy a[] to b[]
sort(b, h);
sort(b+h, n-h);
// Merge two halves in b to a
merge(a,b,n);
return 0;
}void merge(int a[], int b[], int n){
int i=0, j=n/2, k=0;
while(i<=n/2-1 && j<=n-1){
if(b[i] < b[j]){
a[k] = b[i]; i++;
}else{
a[k] = b[j]; j++;
}
k++;
}
if(i==n/2){
while(j<=n-1){
a[k] = b[j];
k++; j++;
}
}
else{
while(i<=n/2-1){
a[k] = b[i];
k++; i++;
}
}
}
Proof By Induction
- 집합 조건을 깰 수 있는 코드는 없다.
편의상 Sort 함수가 끝난 후 정렬된 배열을 b라 했을 때. (이름만 다른 것)

위처럼 집합 조건을 깰 수 있는 코드는 없다. 원소는 동일하다.
Base
n = 1 : 할 일이 없음
원소가 한 개 이므로 정렬을 할 대상이 아니다.
Step
P(n-1) -> P(n) 임을 보이면 된다.
P(n-1) : n/2 일 때 sort() 가 성공
P(n) : n 일 때 sort() 가 성공.
즉 재귀함수 호출이 끝난 후 b[0] < b[1] < .... < b[n/2-1] 이고, b[n/2] < b[n/2 + 1] < ..... <b[n-1] 이라면
n 일 때 sort() 함수가 성공한다 : 함수가 끝난 후 a[0] < a[1] < ...... < a[n-1] 이 성립한다.
이는 Merge 함수의 정확성에 의해, n 일 때 sort 가 성립한다.
merge 함수에서 집합조건을 깰 수 있는 코드는 없고, 정렬된 두 개의 배열을 정렬된 하나의 배열로 합치는 과정이므로 merge 는 참이다.
merge 함수의 시간복잡도 : O(N)
mergeSort 함수는 절반씩 나눠들어가므로, merge 과정을 logN 번 반복했다고 볼 수 있다.
따라서 mergeSort : T(N) : O(NlogN)
시간 복잡도 T(n)
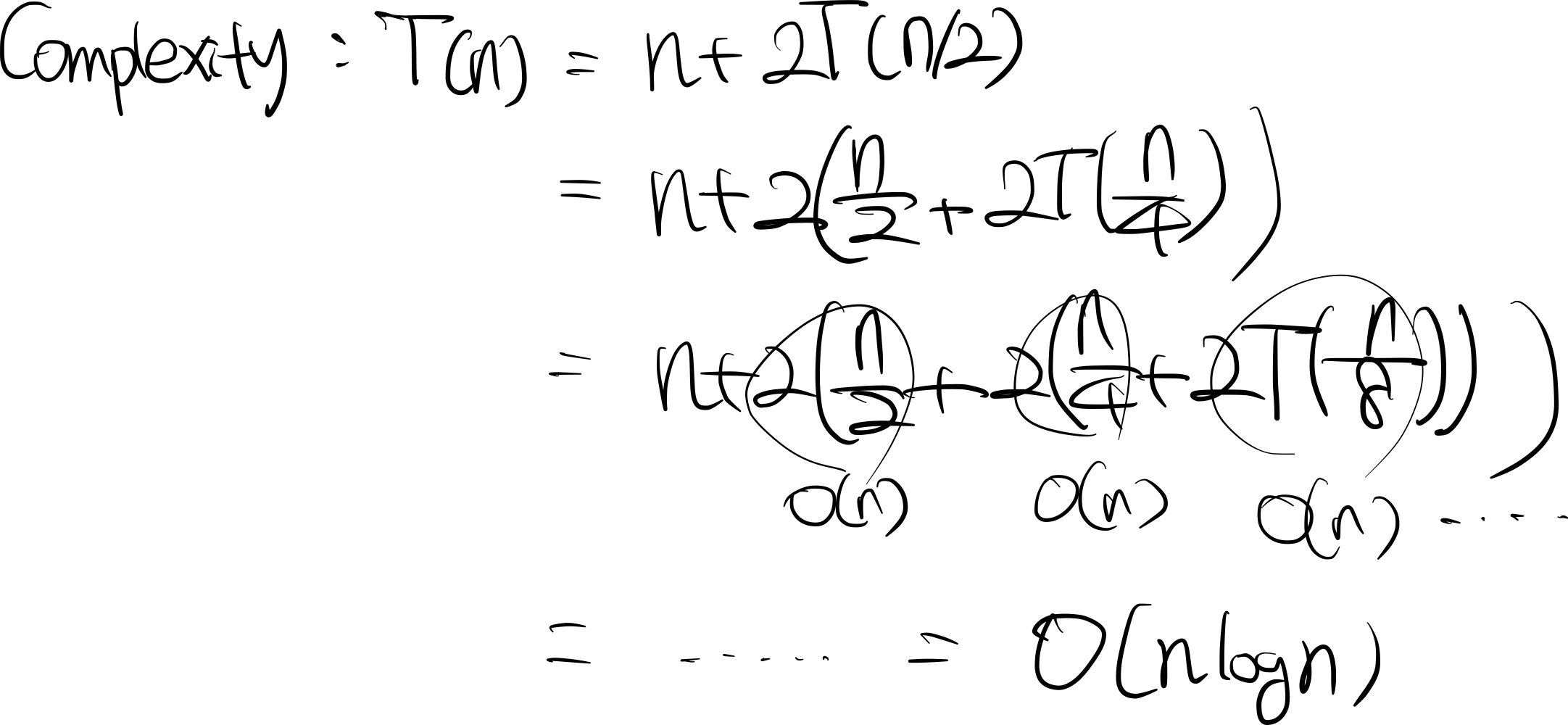
merge 의 시간복잡도가 n . n이 logn 번 반복되므로, nlogn의 시간복잡도를 가진다.
'CS > 자료구조, 알고리즘' 카테고리의 다른 글
| Prim 알고리즘 - 1 (0) | 2022.09.18 |
|---|---|
| Selection Sort 증명 (0) | 2022.09.17 |
| Binary Search 증명 (1) | 2022.09.04 |
| 재귀 알고리즘의 정확성 증명 (0) | 2022.09.03 |
| Halting Problem (정지 문제) (3) | 2022.09.02 |