2022. 9. 19. 13:32ㆍCS/자료구조, 알고리즘
저번 포스팅에서 연결그래프의 MST(Minimum Spanning Tree) 를 구하는 방법인 Prim 알고리즘에 대해 소개하고 그 정확성을 증명해보았습니다.
https://matt1235.tistory.com/51
Prim 알고리즘 - 1
이번 포스팅에서는 Prim Algorithm을 소개하고, 그 정확성을 증명해보고자 한다. 다음 그림을 보자. 정점이 다섯 개가 있고 간선(edge)이 총 10개 있는 연결 그래프이다. 각 간선의 숫자는 노드에서 노
matt1235.tistory.com
이번 포스팅에서는 Prim을 구현해보겠다. => 우선순위 큐를 이용해 구현
우선순위 큐 (Priority Queue)
큐(Queue)는 먼저 들어온 데이터가 먼저 나가는 FIFO(First In First Out) 방식의 자료구조다.
우선순위 큐는 먼저 들어오는 데이터가 아닌, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조이다.
일반적으로 Heap 을 사용해 구현한다.
힙(Heap)
힙은 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조이며 다음과 같은 규칙을 지닌다.
- 모든 노드에 저장된 값(우선순위)은 자식노드보다 크다.
위에 있는 부모 노드일수록 우선순위가 자식보다 커 heap에서 값을 뽑아오면 제일 위에 있는 값이 나오게 된다.
한편 delete를 했으면 다시 남은 노드들을 재배열 해야한다.
문제

위와 연결그래프에서 Prim 알고리즘으로 MST를 찾을 것이다. Prim은 한 노드에서 시작해 인접한 노드들중에서 최소edge를 골르면서 트리를 확장해나간다.
우선순위 큐에서 우선순위가 높을수록 edge 값이 작다고 설정.
=> PriorityQueue에서 뽑은 값을 edge weight 가 작은 값부터 나오게 된다.
TREE 클래스
class TREE{
public:
int a; // 시작 노드
int b; // 도착 노드
int w; // edge 값(무게)
};
TREE를 우선순위 큐에 넣는데, w가 낮은 트리가 heap 위로 오도록 넣으면 된다.
PriorityQueue 도 직접 구현해보도록 하자.
PQ 클래스
class PQ{
public:
TREE arr[1001]; // 1 ~ 1000개까지 가능
int n = 0;
PQ();
void insert(TREE x);
TREE Delete();
void swap(int index);
int isEmpty();
};
swap

index를 인자로 받아 바로 위 부모 노드와 값을 바꾸는 함수.
insert, delete 후에 우선순위 큐를 재정비 할때 쓰는 함수다.
void PQ::swap(int idx){
TREE tmp = arr[idx];
arr[idx] = arr[idx/2];
arr[idx/2] = tmp;
}
insert
void PQ::insert(TREE x){
int i, tmp;
arr[n+1] = x;
i = n +1;
while(i>1 && arr[i].w < arr[i/2].w){
swap(i);
i /= 2;
}
n++;
}삽입을 하게 되면 트리의 맨 마지막 노드에 삽입을 하고, 크기 비교를 해가며 자리를 바꿔준다.
크기가 부모 노드보다 크면 그대로 있고, 더 작으면 위로 올려보낸다. 노드 값이 작은 게 우선순위를 높게 하기로 앞에서 정했기 때문.
Delete
- 완전이진트리 에서 맨 꼭대기 노드를 뽑아냄.
- 맨 아랫노드를 꼭대기로 보낸 후, 다시 크기 비교를 해가며 트리를 재정비한다.
- 트리의 크기는 1 줄어들게 됨

TREE PQ::Delete(){
TREE ret = arr[1];
if(n==1) { n=0; return ret;}
int i;
// 트리의 맨 나중의 원소 값을 맨 꼭대기에 저장.
arr[1] = arr[n];
i = 1; n = n-1;
while(1){
if(2*i > n) // no child
break;
else if(2*i+1 >n){ // only left child
if(arr[2*i].w > arr[i].w){
swap(2*i);
i = 2*i; // 한칸 내려감
}
else break;
}
else{ // left, right child
int cur = arr[i].w;
int l = arr[2*i].w, r = arr[2*i+1].w;
if(cur > l && cur > r){
int j = 0;
if(l < r) j = 2*i;
else j = 2*i + 1;
swap(j);
i=j;
}
else if(cur > l && cur <= r){
swap(2*i);
i = 2*i;
}else if(cur <= l && cur > r){
swap(2*i+1);
i = 2*i+1;
}
else
break;
}
}
return ret;
}삭제는 자식 노드가 더 이상 없을때, 왼쪽 자식만 있을 때, 오른쪽 자식만 있을 때로 경우를 나눠 구현했다.
Insert() 로 TREE를 우선순위 큐에 삽입, delete()로 우선순위 큐의 값을 뽑아온다.
- 뽑은 노드는 edge weight 가 작은 순서대로 나오게 됨.
- 삽입과 삭제 모두 실행 후 트리를 재정비 해주어야 한다.
이렇게 Prim 알고리즘을 구현해 보았다.
전체 소스코드
#include <iostream>
#include <vector>
using namespace std;
class TREE{
public:
int a; // 시작 노드
int b; // 도착 노드
int w; // edge 값(무게)
};
class PQ{
public:
TREE arr[1001]; // 1 ~ 1000개까지 가능
int n = 0;
PQ();
void insert(TREE x);
TREE Delete();
void swap(int index);
int isEmpty();
};
PQ::PQ(){
n = 0;
}
int PQ::isEmpty(){
return n==0;
}
void PQ::swap(int idx){
TREE tmp = arr[idx];
arr[idx] = arr[idx/2];
arr[idx/2] = tmp;
}
void PQ::insert(TREE x){
int i, tmp;
arr[n+1] = x;
i = n +1;
while(i>1 && arr[i].w < arr[i/2].w){
swap(i);
i /= 2;
}
n++;
}
TREE PQ::Delete(){
TREE ret = arr[1];
if(n==1) { n=0; return ret;}
int i;
// 트리의 맨 나중의 원소 값을 맨 꼭대기에 저장.
arr[1] = arr[n];
i = 1; n = n-1;
while(1){
if(2*i > n) // no child
break;
else if(2*i+1 >n){ // only left child
if(arr[2*i].w > arr[i].w){
swap(2*i);
i = 2*i; // 한칸 내려감
}
else break;
}
else{ // left, right child
int cur = arr[i].w;
int l = arr[2*i].w, r = arr[2*i+1].w;
if(cur > l && cur > r){
int j = 0;
if(l < r) j = 2*i;
else j = 2*i + 1;
swap(j);
i=j;
}
else if(cur > l && cur <= r){
swap(2*i);
i = 2*i;
}else if(cur <= l && cur > r){
swap(2*i+1);
i = 2*i+1;
}
else
break;
}
}
return ret;
}
PQ pq;
vector<pair<int, int>> edges[1000];
int M[1000];
int main(){
int n, m, c; // node, edge, curNode
cin >>n >>m;
for(int i=0;i<m;i++){
int a,b,w;
cin >> a >>b >>w;
edges[a].push_back(make_pair(b,w));
edges[b].push_back(make_pair(a,w));
}
cout <<"탐색을 시작하려는 노드를 입력해주세요 : ";
cin >> c;
M[c] = 1;
for(int i=0;i<edges[c].size();i++){
TREE x;
x.a = c;
x.b = edges[c][i].first;
x.w = edges[c][i].second;
pq.insert(x);
}
while(!pq.isEmpty()){
TREE y = pq.Delete();
TREE tmp;
if(M[y.a]==1 && M[y.b]==1){ // 이미 방문한 두 노드를 이어버리면 Cycle생김. tree에 위배됨!
continue;
}else{
M[y.a] =1, M[y.b] = 1;
printf("edge from Node %d to Node %d of weight %d Selected.\n",y.a, y.b, y.w);
c = y.b; // curNode
for(int i=0;i<edges[c].size();i++){
tmp.a = c;
tmp.b = edges[c][i].first;
tmp.w = edges[c][i].second;
pq.insert(tmp);
}
}
}
return 0;
}
입력 예시, 실핼 결과
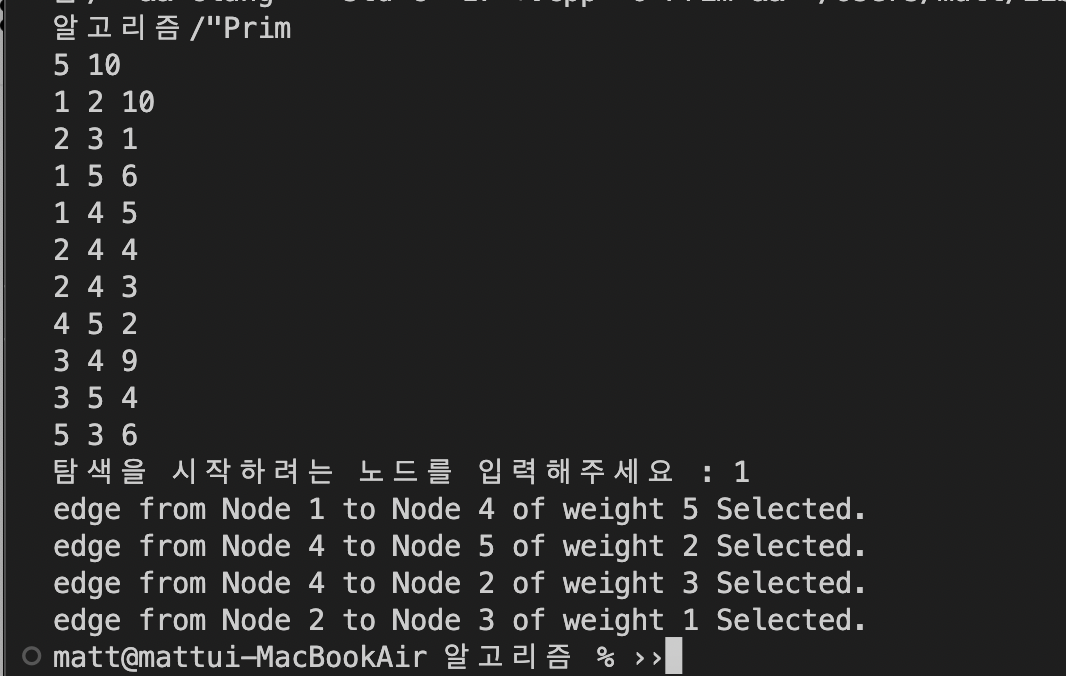
알맞게 동작함을 확인할 수 있다.
'CS > 자료구조, 알고리즘' 카테고리의 다른 글
| 다익스트라(Dijkstra) 정확성 증명 (1) | 2022.10.06 |
|---|---|
| Kruskal 알고리즘 (Greedy) (0) | 2022.09.24 |
| Prim 알고리즘 - 1 (0) | 2022.09.18 |
| Selection Sort 증명 (0) | 2022.09.17 |
| Mergesort (0) | 2022.09.12 |