2022. 9. 24. 11:54ㆍCS/자료구조, 알고리즘
Shortest Path 를 찾는 알고리즘으로 Prim 알고리즘을 살펴보았다.
prim 은 그리디 알고리즘으로, MST(최소 신장 트리)를 만들기 위해 힙, 즉 우선순위큐를 사용했다.
두 정점 사이의 edge 거리가 작은 것 우선순위가 높도록 정했다.
이번 포스팅에서 다룰 Kruskal 알고리즘도 Shortest path를 찾는 문제다. 연결 그래프가 주어지고 MST를 구하면 되는 문제이다.
Prim 알고리즘과 목적이 같지만, 구현 방법에 약간의 차이가 있다.
Prim 알고리즘 포스팅: https://matt1235.tistory.com/51
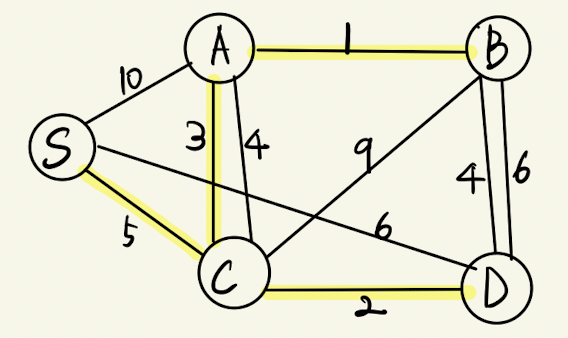
문제)
다음과 같은 연결그래프가 있다. 모든 정점을 연결하는 Minimum Spanning Tree를 구하라.
Prim 알고리즘은 T라는 해집합을 점차 늘려나가는 식으로 정답을 구했다. Prim에서는 알고리즘이 T에 인접한 edge들 중 최솟값을 싸이클이 생기지 않게 골랐다. 즉 T라는 현재 트리에서 뻗어가는 식으로 정답을 구했다.
크루스칼 알고리즘이 Prim 과 다른점은 현재 구하고 있는 트리에 인접한 edge를 더하는 것이 아닌, 그래프에 존재하는 최소 edge 를 골라 더하는게 끝이다.
MST의 특성 상 노드가 N 개 일 때 edges는 N-1 개인 것은 확정이다.
Kruskal Algorithm 동작 방식
- keep adding edges
- As long as no cycle results
- Until N-1 Edges are added
Prim과 다르게 트리에서 뻗어나가는데 아닌, 중구난방으로 가중치가 최소인 간선들을 더한다.
Union & Find
Kruskal 알고리즘에는 Union Find 알고리즘이 필요하다.
노드가 어떤 덩어리에 속하는지? -> 부모 노드가 뭔지를 알아야 한다.
이유
Kruskal 에서 새로 추가할 edge의 양끝 노드들이 같은 집합에 속해 있는지를 검사하기 위함이다. (사이클 형성 여부 확인)
예를 들어 정점 A, B가 있는데 두 정점이 같은 집합에 속한다고 하자. 즉 두 정점의 부모 노드가 P로 같다.
같은 집합에 속한다는 것은 스패닝트리를 이루고 있다는 뜻 A, B 정점은 연결되어 있다는 뜻이다.
A,B의 부모노드가 P로 같다면, 이 두 정점을 연결하는 것은 싸이클을 형성하게 되므로 연결해서는 안된다.
위와 같이 싸이클 생성 여부를 판단하기 위해 Union, Find 가 필요하다.
Union Find 구현
#define N 10
int p[11];
/**
* Kruskal Union-Find ALgorithm
* */
int find(int x){ // 노드 x의 부도 노드를 찾아줌.
if(x==p[x]) return x;
else
return p[x] = find(p[x]);
}
void Union(int x, int y){
x = find(x); // x의 parent
y = find(y); // y의 parent
if(x != y){
if(x<y) p[y] = x;
else p[x] = y;
}
}
bool isSameParent(int x, int y){
x = find(x);
y = find(y);
if(x == y) return true;
else return false;
}find로 부모 노드를 찾아준다.
Union 함수로 두 정점을 연결할 경우에 호출. 두 정점이 속하는 집합의 Parent를 같게 만들어준다.
isSameParent 는 두 정점이 같은 부노 노드를 가지는지를 판별해주는 함수이다.
알고리즘의 정확성 증명
Kruskal 의 정확성을 증명해보자. 이는 Prim의 정확성 증명과 유사하다.
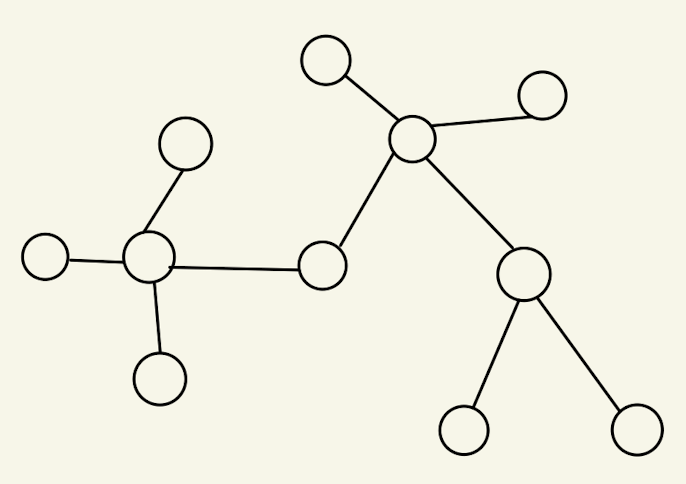
위 그림을 우리가 구하려는 답 중 하나인 T(mst)라고 하자. ( T(mst)는 정답들 중 하나. )
T는 알고리즘이 진행되면서 만드는 답으로, edge set 이다.
Proof By Invariant
Invariant : T ⊆ T(mst)
T(mst)는 정답 중 하나이다. (정답은 여러개가 있을 수 있음)
위 불변조건이 깨지지 않고 항상 성립할 때, Kruskal 알고리즘이 정상 작동한다는 것을 증명할 수 있다.
Invariant 를 수학적 귀납법으로 증명하자.
proof By Induction
Assume : |T| = k 일 때 T ⊆ T(mst) 가 성립한다고 가정.
Base ) k= 0.
아직 아무것도 고르지 않은 상태이다. 확인할 게 없음... => OK(성립)
Step) T U {e} = T'
이 때도 우리가 설정한 Invariant 가 성립함을 보이면 된다.
Case 1. T' ⊆ T(mst) : OK
알고리즘이 고른 e 가 처음 가정한 T(mst)의 부분집합인 경우. -> 성립함
Case 2. T' ⊄T(mst)
T U {e}에 e 를 포함한 사이클이 존재하게 된다. 알고리즘의 로직은 싸이클을 만들지 못하므로 T(mst) 의 관점에서 보았을때의 얘기다.
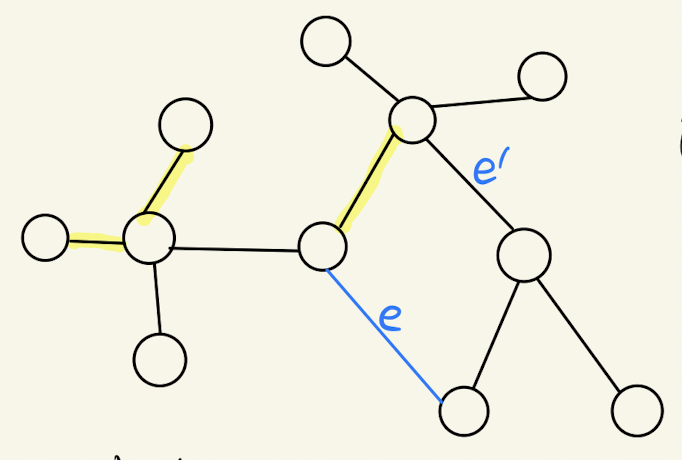
- 노란색으로 칠해진 부분 : T
- e : 알고리즘이 고른 간선
- e' : 싸이클 안에 T에 속하지 않는 edge.
e와 e'의 가중치(weight)값을 비교해보자.
case 2-1) w(e) < w(e')
e'의 weight 가 e의 weight 보다 큰 경우.
(T(mst) - {e'}) U {e} : 더 좋은 답이 된다. → 모순! T(mst)는 애초에 답이 아니었다.
case 2-2) w(e) > w(e')
알고리즘은 edge 가 작은순으로 골라 T에 포함시킨다. 애초에 e보다 e'이 먼저 골라졌을 것. → 모순
case 2-3) w(e) = w(e')
( T - {e'} ) U {e} 도 정답이 된다. 이 경우는 우리가 처음에 설정했던 T(mst)는 아니지만 또 다른 정답이 된다.
즉 T는 T(mst)에 포함되므로 Invariant는 성립한다.
따라서 귀납적으로 Invariant는 어디에서도 깨지지 않음을 알 수 있다. 따라서 Kruskal 알고리즘의 정확성은 증명되었다.
전체 소스코드
#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;
#define N 10
int p[11];
vector<pair<int, int>> a;
class TRI{
public:
int a;
int b;
int w;
};
class PQ{
public:
int n;
TRI arr[1001]; // index 1~1000
void insert(TRI x);
TRI pop();
PQ();
bool isEmpty();
void swap(int x);
};
bool PQ::isEmpty(){
return n==0;
}
PQ::PQ(){
n = 0;
}
void PQ::swap(int x){
TRI temp = arr[x/2];
arr[x/2] = arr[x];
arr[x] = temp;
}
void PQ::insert(TRI x){
arr[n+1] = x;
int i = n+1;
while(i>1 && arr[i].w > arr[i/2].w){
swap(i);
i = i/2;
}
n++;
}
TRI PQ::pop(){
TRI tmp = arr[1];
arr[1] = arr[n];
n--;
int i = 1;
while(1){
if(2*i > n) break;
else if(2*i + 1 > n) { // onlt left child
if(arr[i].w > arr[2*i].w) {
swap(2*i);
i = 2*i;
}else{
break;
}
}
else { // left, right child
if(arr[i].w > arr[2*i].w && arr[i].w > arr[2*i-1].w){
if(arr[2*i].w > arr[2*i+1].w)
swap(2*i+1);
else
swap(2*i);
i *= 2;
}
else if(arr[i].w > arr[2*i].w && arr[i].w < arr[2*i+1].w){
swap(2*i+1);
i *= 2;
}
else if(arr[i].w < arr[2*i].w && arr[i].w > arr[2*i+1].w){
swap(2*i); i*=2;
}
else break;
}
}
return tmp;
}
/**
* Kruskal Union-Find ALgorithm
* */
int find(int x){ // 노드 x의 부도 노드를 찾아줌.
if(x==p[x]) return x;
else
return p[x] = find(p[x]);
}
void Union(int x, int y){
x = find(x); // x의 parent
y = find(y); // y의 parent
if(x != y){
if(x<y) p[y] = x;
else p[x] = y;
}
}
bool isSameParent(int x, int y){
x = find(x);
y = find(y);
if(x == y) return true;
else return false;
}
int main(){
for(int i=1;i<=N;i++)
p[i] = i;
a.push_back(make_pair(3,2));
a.push_back(make_pair(3,5));
a.push_back(make_pair(2,4));
a.push_back(make_pair(4,1));
a.push_back(make_pair(7,6));
a.push_back(make_pair(7,9));
a.push_back(make_pair(7,8));
a.push_back(make_pair(10,1));
for(int i=0;i<a.size();i++){
Union(a[i].first, a[i].second);
}
for(int i=1;i<=10;i++){
cout << p[i] << " ";
}cout << endl;
cout << isSameParent(1,5) << endl;
cout << isSameParent(9,8) << endl;
return 0;
}'CS > 자료구조, 알고리즘' 카테고리의 다른 글
| Quick Sort (2) | 2022.10.13 |
|---|---|
| 다익스트라(Dijkstra) 정확성 증명 (1) | 2022.10.06 |
| Prim 알고리즘 - 2 (2) | 2022.09.19 |
| Prim 알고리즘 - 1 (0) | 2022.09.18 |
| Selection Sort 증명 (0) | 2022.09.17 |